LA RACIONALIZACION
La racionalización de radicales es un proceso donde se tiene que eliminar el radical o los radicales, que están en el denominador de la fracción.
Racionalizar una fracción con raíces en el denominador, es encontrar otra expresión equivalente que no tenga raíces en el denominador. Para ello se multiplica el numerador y el denominador por la expresión adecuada, de forma que al operar elimine la raíz del denominador.
Racionalización de un radical índice 2
Para racionalizar un monomio de este tipo, se debe multiplicar el numerador y el denominador de la fracción por el denominador de la misma. En el siguiente caso:

Racionalización de binomio de índice 2
Para racionalizar un binomio de índice 2, se debe hacer un proceso similar al ejercicio anterior, multiplicar el numerador y denominador de la fracción por el denominador de la misma. En el siguiente ejemplo: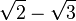 ; este resultado es el que da el producto notable de los binomios conjugados.
; este resultado es el que da el producto notable de los binomios conjugados. ·
· 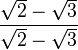 =
= 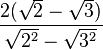
Ahora, se procede al despeje de las raíces cuadradas del denominador:
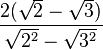 =
= 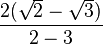
 =
= 
Racionalización de monomios con índices mayores que 2:
Tómese el siguiente caso, ya que tenemos numeradores y denominadores fraccionados y multiplicados por indices mayores que 3.![\frac{{2}}{\sqrt[5]{8a^3b^4}}](http://upload.wikimedia.org/math/2/8/b/28b560d173a879a45f5a697d212ec501.png) =
= ![\frac{{2}}{\sqrt[5]{2^3a^3b^4}}](http://upload.wikimedia.org/math/8/1/a/81a07829eb2a526acc5c99c442f8095e.png)
Las cantidades exponenciales de los subradicales del radical para multiplicar al numerador y denominador de la fracción será el número del exponente que falta para acercarse al índice del radical. En caso de que el exponente sea mayor que el índice de la raíz, la cantidad de aquel exponente será la que falte para llegar al múltiplo más cercano de la raíz.
![\sqrt[5]{2^3a^3b^4}](http://upload.wikimedia.org/math/6/1/a/61a85ad591337a262827c9f70a243502.png) =
= ![\sqrt[5]{2^2a^2b}](http://upload.wikimedia.org/math/d/f/0/df02d0fc08b6bcf7796710b87403d98a.png)
![\sqrt[5] {2^2a^2b}](http://upload.wikimedia.org/math/d/f/0/df02d0fc08b6bcf7796710b87403d98a.png) , ya que éste es el radical que al ser multiplicado por el denominador los exponentes de las cantidades subradicales serán iguales al índice de la raíz...
, ya que éste es el radical que al ser multiplicado por el denominador los exponentes de las cantidades subradicales serán iguales al índice de la raíz...Ahora, se procede a multiplicar el numerador y el denominador:
![\frac{{2}}{\sqrt[5]{2^3a^3b^4}}](http://upload.wikimedia.org/math/8/1/a/81a07829eb2a526acc5c99c442f8095e.png) ·
· ![\frac{\sqrt[5] {2^2a^2b} }{\sqrt[5]{2^2a^2b}}](http://upload.wikimedia.org/math/8/9/3/89315c6b50c3027d25e1f1e95b61d6fd.png) =
= ![\frac{{2\sqrt[5]{2^2a^2b}}}{\sqrt[5]{2^5a^5b^5}}](http://upload.wikimedia.org/math/e/3/9/e393322e7e2301bdd0c26b9df0405992.png)
![\frac{{2\sqrt[5]{2^2a^2b}}}{\sqrt[5]{2^5a^5b^5}}](http://upload.wikimedia.org/math/e/3/9/e393322e7e2301bdd0c26b9df0405992.png) =
= ![\frac{{2\sqrt[5]{4a^2b}}}{{2ab}}](http://upload.wikimedia.org/math/1/5/7/157186c3d733b0a6317bfe11b3bbd31a.png)
![\frac{{2\sqrt[5]{4a^2b}}}{{2ab}}](http://upload.wikimedia.org/math/1/5/7/157186c3d733b0a6317bfe11b3bbd31a.png) =
= ![\frac{{\sqrt[5]{4a^2b}}}{{ab}}](http://upload.wikimedia.org/math/a/a/4/aa4f5f2ff57625eeecb4f8ca585d8d45.png)
Racionalización de binomios con radical mayor a 2
Cuando se tienen binomios con radical de índice 3, es preciso utilizar productos notables,en este caso la adición y sustracción de cubos, según sea el caso. Por ejemplo, en el caso de la expresión:
![\sqrt[3]{a}-\sqrt[3]{b}](http://upload.wikimedia.org/math/1/1/4/1142fc632406f730c6d150aba9b08a5e.png) =
= ![(\sqrt[3]{a})^2 + \sqrt[3]{a}\sqrt[3]{b} + (\sqrt[3]{b})^2](http://upload.wikimedia.org/math/c/a/f/caf7cb9108314ed9a5b309cb1235dcfb.png)
![\frac{{1}}{\sqrt[3]{a}-\sqrt[3]{b}}](http://upload.wikimedia.org/math/b/4/b/b4bb468eebe86398e4e66a6e93c2d59b.png) ·
· ![\frac{(\sqrt[3]{a})^2 + \sqrt[3]{a}\sqrt[3]{b} + (\sqrt[3]{b})^2}{(\sqrt[3]{a})^2 + \sqrt[3]{a}\sqrt[3]{b} + (\sqrt[3]{b})^2}](http://upload.wikimedia.org/math/f/3/d/f3d325f5dce87a6e21a2af8027a5debe.png) =
= ![\frac{{(\sqrt[3]{a})^2 + \sqrt[3]{a}\sqrt[3]{b} + (\sqrt[3]{b})^2}}{{\sqrt[3]{a}-\sqrt[3]{b}}[(\sqrt[3]{a})^2 + \sqrt[3]{a}\sqrt[3]{b} + (\sqrt[3]{b})^2]}](http://upload.wikimedia.org/math/3/2/1/32167c56f8a46e43d17e8478fa3c0324.png)
![=\frac{{\sqrt[3]{a^2} + \sqrt[3]{ab}+ \sqrt[3]{b^2}}}{{\sqrt[3]{a}-\sqrt[3]{b}}[(\sqrt[3]{a})^2 + \sqrt[3]{a}\sqrt[3]{b} + (\sqrt[3]{b})^2]}](http://upload.wikimedia.org/math/1/b/4/1b421592db8b893f459c4380a5861546.png) :
:![=\frac{{\sqrt[3]{a^2} + \sqrt[3]{ab}+ \sqrt[3]{b^2}}}{{\sqrt[3]{a^3}-\sqrt[3]{b^3}}}](http://upload.wikimedia.org/math/b/7/f/b7fd664a27078df36f15a208dd527cd1.png)
![=\frac{{\sqrt[3]{a^2} + \sqrt[3]{ab}+ \sqrt[3]{b^2}}}{{\sqrt[3]{a^3}-\sqrt[3]{b^3}}}](http://upload.wikimedia.org/math/b/7/f/b7fd664a27078df36f15a208dd527cd1.png) :
:![=\frac{{\sqrt[3]{a^2} + \sqrt[3]{ab}+ \sqrt[3]{b^2}}}{{{a}-{b}}}](http://upload.wikimedia.org/math/c/3/e/c3e19904d502db9a3af54f1e4891c9b1.png)



![\frac{{\sqrt[3]{a^2} + \sqrt[3]{ab}+ \sqrt[3]{b^2}}}{{\sqrt[3]{a}-\sqrt[3]{b}}[(\sqrt[3]{a})^2 + \sqrt[3]{a}\sqrt[3]{b} + (\sqrt[3]{b})^2]}](http://upload.wikimedia.org/math/0/f/a/0fac0bbf902061f2a0eab6ab1e47b660.png)
pura wikipedia
ResponderEliminarsisa
EliminarRacionalizar 1/raiz octava de x^12
ResponderEliminarRacionalizar 1/raiz octava de x^12
ResponderEliminar